I was reading through Google's aptitude tests, and among the questions, this one stuck on my head... Later as I walked to the bus station came up with the answer.
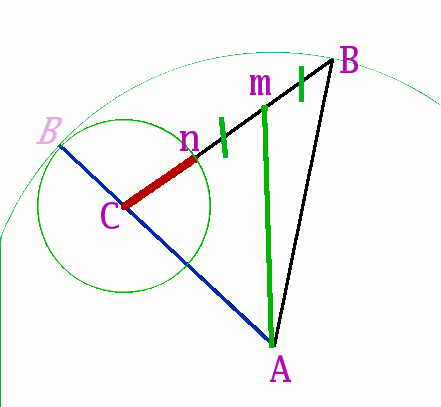
Given a triangle ABC, how would you use only a compass and straight edge to find a point M such that triangles ABM, ACM, and BCM have equal perimeters? (Assume that ABC is constructed so that a solution does exist.)
Once you realize that the line AM is the same for both, then the problem is only to divide ABC's permieter in 2 equal parts. This is how it works..
-
Choose either AB or AC, I chose AB, which is the longest in this case, it works the same way if you choose the shortest.
-
With your compass draw the arc with radius AB
-
Prolong AC until it reaches the arc with radius AB (point B'), this extra segment is how much it takes to make AC the same length as AB
-
Again, with your compass, draw an arc over BC with radius CB', This point is N, so now AC + CN = AB
-
Using your compass one last time, plot M at the midpoint of NB
-
With your straightedge, draw AM
-
Triangles ABM and ACM should have the same perimeter :)
Then I also figured that you could come with some interesting relationship if you had the patience to solve using Heron's formula :P.
Comments
#2030" title="2006-09-07 01:05:25">Droper: cool!, y remember my classes in pitagoras :D
#2035" title="2006-09-07 21:22:52">cachete: demasiada geekness...
#2037" title="2006-09-08 12:06:59">E666: what about triangle BCM perimeter's?
#2040" title="2006-09-08 15:21:53">Jj: Or just rotate the vertex labels :P
#2042" title="2006-09-08 18:50:01">E666: what about triangle BCM perimeter’s!
#2104" title="2006-09-10 23:38:12">Orgen: Cierto. El problema pide que los perÃmetros de los tres triángulos formados sean iguales y, en esta solución, el perÃmetro del triángulo BCM (2*BC) no es igual al de los triángulos ABM y ACM.
#2127" title="2006-09-12 00:48:53">Jj: The correct answer can be found at http://jj.isgeek.net/2006/09/12/google%e2%80%99s-triangle-problem-correction/
