Google's triangle problem (Correction)

It is always the same reason I fail in exams, I never read the whole thing, on my last post about Google's problem I TOTALLY skipped the third triangle BCM, which my friend Enrique Llanos #comment-2035">pointed out :P

This time, the solution is not as easy as the first one. So I ran to the Triangle Centers Encyclopedia to look for an answer :D, and to my surprise I find the Isoperimetric center! which is the poiint at which the perimeters of the new triangles have the same perimeters.

The tricky part is that, This point is located at the center of the outer Soddy circle, those who followed the Heron's formula link, must have run into these circles before.

The fun begins

The fun is that the construction of this outer circle is not a trivial task, or at least not trivial to me :(, I couldn't come up with the answer, so Dr Math gave me little help :)

Here the solution:

Start with a random triangle and the required tools.

Starting triangle

With some geometry from school, we find the inscribed circle.

Incircle found

And after following some almost random instructions... you find the Outer Soddy Circle.

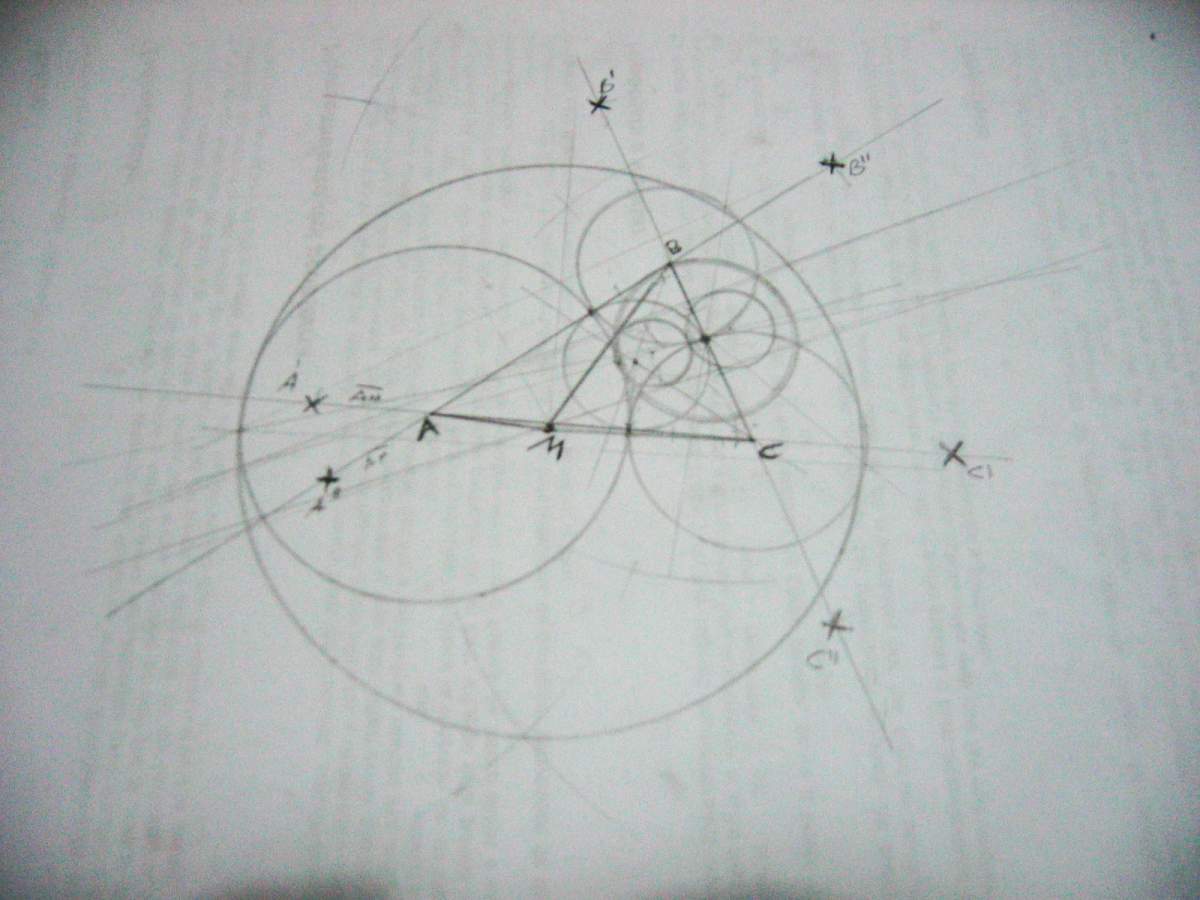
Outer Soddy circle found!!

My random triangle had the Isometric center outside of the triangle very close to the side AC.

Proof that the triangles AMB, AMC and BMC have equal perimeters is found in lines A'C', B' C" and A"B"

Well, I didn't come up with the answer, but the least I could do is find it :P

Comments

#2193" title="2006-09-14 09:24:46">E666: "Let no one enter who does not know geometry".